1. Произвольный вектор а может быть представлен в системе орт i, j, k следующей формулой
,
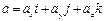где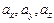 
- проекции вектора ана соответствующие координатные оси. Если даны точки M1 (x1;y1;z1) и M2 (x2;y2;z2), то проекции вектора 
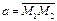на координатные оси находятся по формулам
; 
; 
.
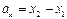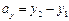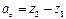2. Модуль вектора 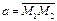вычисляется по формуле
.
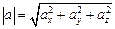3. Косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей.
.
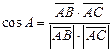4. Проекция вектора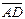 
на вектор 
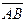равна скалярному произведению этих векторов, деленному на модуль вектора 
:
.
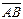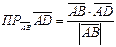5. Векторное произведение векторов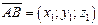 
и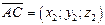 
находится по формуле
.
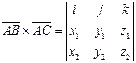6. Объем параллелепипеда, построенного на трех некомпланарных векторах , ,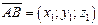 
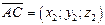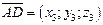, равен абсолютной величине их смешанного произведения 
.
.
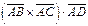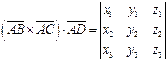