Виды погрешности: 1. неустранимая погрешность или погрешность исходной информации (сумма погрешности математической модели и погрешности исходных данных),2.погрешность метода или погрешность аппроксимации (порождается применяемым приближенным методом решения)3.вычислительная погрешность или погрешность округления (результат конечности разрядной сетки сумматора). Исследуем погрешность аппроксимации на примере метода итераций.
Предположим, что условия теоремы о сходимости выполнены и метод итераций сходится. Оценим по модулю разность между корнем x и приближением xn+1. Учитывая теорему Лагранжа, неравенства 0<q<1 и неравенство для модуля суммы, получим:
│ξ - xn+1│=│j(ξ) - j(xn)│=│j¢(η)│×│x-xn│£q│x-xn│£
£ q│(x-xn+1)+(xn+1-xn)│£ q│x-xn+1│+q│xn+1-xn│.
Окончательно имеем │ξ - xn+1│≤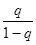 
│xn+1-x n│.
Если 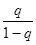≤1 (при q£0.5), то│ξ - xn+1│≤│xn+1-x n│. Это означает, что если в процессе итераций выполнилось условие │xn+1-xn│£ ε, то и│ξ - xn+1│≤e. Если же, например, q=0.9, то = 
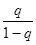=9, поэтому │ξ - xn+1│≤9│xn+1-xn│, т.е. при выполнении неравенства │xn+1-xn│£ ε близость xn+1 к корню ξ оценивается только величиной в 9e. Вообще, чем q ближе к единице, тем метод итераций сходится медленнее.
