Схема алгоритма метода трапеций.

30.) Численное интегрирование — вычисление значения определённого интеграла.

Численное интегрирование применяется, когда:

1. Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.

2. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, .

Если функция непрерывна на отрезке [a, b] и ее первообразная может быть определена через известную функцию, то вычисление такого интеграла производится по формуле Ньютона – Лейбница:

.

Алгоритм получения определенного интеграла:

1)Сначала вычисляют значения функции f(x_i) = y_i в некоторых узлах x_i Î[a, b].

2)Затем выбирается интерполяционный многочлен P(x), проходящий через полученные точки (x_i, y_i), который используется при вычислении приближенного значения интеграла :

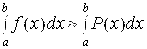
При реализации такого подхода формулы численного интегрирования принимают следующий общий вид:

,где - узлы интерполирования, A_i – некоторые коэффициенты, R – остаточный член, характеризующий погрешность формулы.(квадратурная формула)