Схема Эйткена предлагает более удобную форму нахождения полинома Лагранжа:
На первом этапе вычисляются многочлены L0,1(x), L1,2(x), :, Ln-1,n(x), построенные на каждой паре соседних узлов 0,1; 1,2; :; n-1,n соответственно.
При этом 
, 
, :, 
.
Таким образом, многочлены, построенные на паре соседних узлов, вычисляются по формулам: 
.
Затем на основе этих многочленов вычисляются многочлены, построенные на тройках соседних узлов: 
.
И т.д. пока не получится один многочлен, построенный на всех узлах интерполяции: 
.
Полученный многочлен L0, 1, ..., n(x)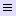 
Ln(x).
