3. Дополнение к множеству. Разность множеств.
Пусть В – подмножество множества А. множество всех элементов из А, не принадлежащих множеству В, называют дополнением к подмножеству В и обозначают В/А. Так , если А множество учащихся в некотором классе, а В –множество девочек в нем, то В/А есть множество мальчиков в этом классе.
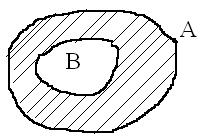Если В А, то на диаграмме Эйлера – Венна множеству В/А принадлежат все точки множества А, на принадлежащие В. На рис множество В/А заштриховано.
Для любых подмножеств А и В универсального множества I имеют место следующие равенства:
1) (А∩В)/ = А/ U В/;
2) (АUB)/ = А/ ∩ В/.
Разностью двух множеств А и В называется такое множество Х= А-В , в которое входят все те элементы, которые принадлежат А и не принадлежат В.
Обозначение А\ B .
Пример: если А = {a,b,c.d,e} , а В={b,d,e,k,f,n}, то А\ B = {a,c}
=> А\ B = А\ (А∩В) При вычитании множества В из множества А из А удаляется пересечение А и В. А-В = А-АВ
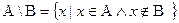Так как любой элемент х из множества А\ B обладает свойством « х принадлежит А и не принадлежит В», то определение разности множеств А и В можно записать так:
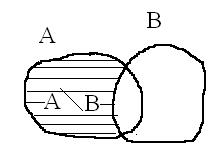На рис множество А\ B заштриховано.
Для любых множеств А,В,С справедливы следующие равенства, связывающие вычитание множеств с другими операциями над множествами:
а)А\(В∩С) = (А\В)U(А\С)
б) А\(ВUС) = (А\В)∩ (А\С)
