Первая улучшенная формула Эйлера
Особенности метода Эйлера.
Метод очень прост в реализации, но обладает малой точностью, поскольку погрешность каждого нового шага систематически возрастает. Существует модификации метода, повышающие его точность, - методы Эйлера-Коши – первая и вторая улучшенные формулы.
Пусть дано дифференциальное уравнение:
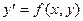
с начальными условиями:
.
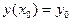Решение в каждой точке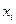 
определяется по формуле:
,
где
.
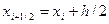
Геометрически это означает, что отрезок ломанная между точками 
заменяется на два отрезка 
. Направление первого отрезка совпадает с направлением интегральной кривой в точке
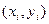, а направление второго отрезка определяется направлением, интегральной кривой в вспомогательной точке
.
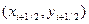Пример.
Пусть дано дифференциальное уравнение:
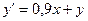
с начальными условиями:
.
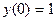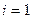
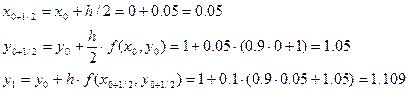
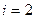
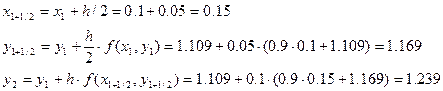
Решение ОДУ имеет вид:
| 
|
| 0.0
| 1.000
|
| 0.1
| 1.109
|
| 0.2
| 1.239
|
Пусть дано дифференциальное уравнение:
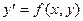
с начальными условиями:
.
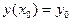Решение в каждой точке 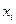определяется по формуле:
,
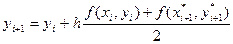где
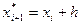
Геометрически это означает, что определяется направление интегральной кривой в исходной точке 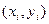и во вспомогательной точке 
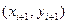, а в качестве окончательного направления ломаной берется среднее этих направлений.
Пример.
Пусть дано дифференциальное уравнение:
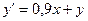
с начальными условиями:
.
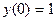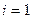
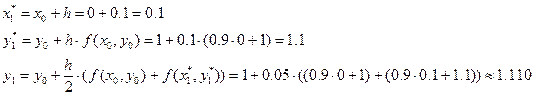
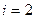
Решение ОДУ имеет вид:
|
|
|
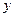
| 0.0
| 1.000
|
| 0.1
| 1.110
|
| 0.2
| 1.241
|
