Численные методы решения обыкновенных дифференциальных уравнений.
В основе метода Эйлера (метод ломаных) лежит идея графического построения решения дифференциальных уравнений, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
Пусть дано дифференциальное уравнение:
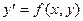
с начальными условиями:
.
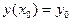Выбрав достаточно малый шаг h, строится система равноотстоящих точек 
.
В методе Эйлера приближенные значения 
вычисляются последовательно по формулам:
.
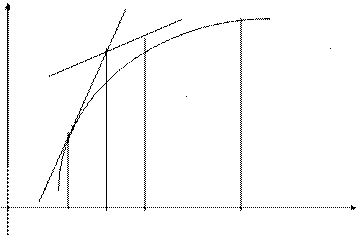
При этом искомая интегральная кривая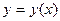 
, проходящая через точку
, заменяется ломанной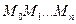 
с вершинами 
; каждое звено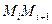 
этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения 
, которая проходит через точку 
y
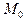
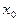
Пример
Пусть дано дифференциальное уравнение:
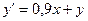
с начальными условиями:
.
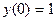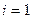
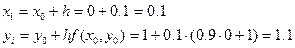
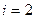
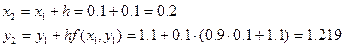
Решение ОДУ имеет вид:
| 
|
| 0.0
| 1.000
|
| 0.1
| 1.100
|
| 0.2
| 1.219
|
