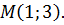Предел функции двух переменных.
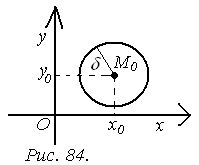Зафиксируем на координатной плоскости 
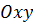некоторую точку 
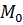с координатами 
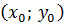. Множество всех точек 
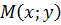, удовлетворяющих неравенству
называется 
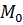- окрестностью точки (рис. 84).
Пусть функция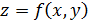 
определена в некоторой окрестности точки 
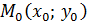за исключением может быть самой этой точки. Число 
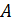называется пределом функци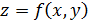и при
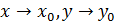, если для любого числа 
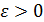существует такое число 
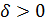, что из неравенства
следует неравенство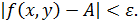 
В этом случае записывают
Из этого определения следует, что если предел существует, то он не зависит от пути, по которому точка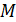 
стремится к точке 
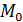. Для функции одной переменной точка 
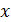может стремиться к точке 
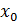только двумя путями: слева и справа. На плоскости таких направлений бесконечно много (рис. 85). Основные свойства предела функции двух переменных аналогичны соответствующим свойствам пределов функции одной переменной.
Функция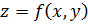 
называется непрерывной в точке 
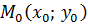если она:
1) определена в этой точке и в некоторой ее окрестности;
2) имеет предел в этой точке, равный её значению в ней:
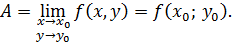
Функция непрерывная в каждой точке некоторой области называется непрерывной в этой области. Можно показать, что функция 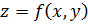будет непрерывна в точке 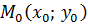тогда и только тогда, когда
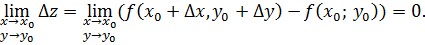
Точки, в которых условие непрерывности не выполняются, называются точками разрыва.
Пример 65. Функция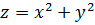 
не имеет точек разрыва на всей координатной плоскости, а функция
имеет разрыв в точке 
