Для вычисления значения интеграла разбиваем отрезок интегрирования на n равных частей (в первом приближении принимаем n = 4) и определим значения f (xi) (i = 0, 1, …, n), где xi = a + h×i; h = (b – a)/n (рисунок 3).
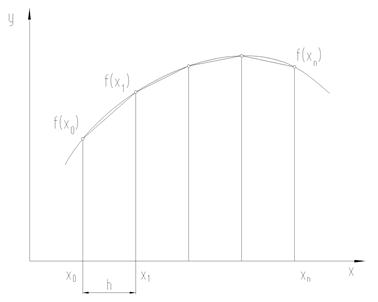
Рисунок 3 – Метод трапеций
Вычислим площадь si каждой из полученных трапеций: si = h×(f (xi-1) + f (xi))/2 . Сумма I1площадей этих трапеций и является
Однако одно приближение не позволяет оценить точность, с которой вычислено значение интеграла, поэтому необходимо найти второе приближение. Для этого увеличим число отрезков разбиения n в 2 раза, т. е. n = 2×n. Аналогично I1 находим
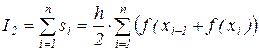 .
.
Для вычисления интеграла с заданной точностью e проверим условие |I2 - I1| £ e. Если условие выполняется, то I2 принимается за искомое значение интеграла. Если условие не выполняется, то последнее значение интеграла I2 принимается за предыдущее, т. е. I1 = I2. После этого удвоим число точек деления отрезка и вычислим новое значение I2. Процесс удвоения n и вычисление I2 будем продолжать до тех пор, пока не выполнится условие |I2 - I1| £ e.