Рассмотрим графическую иллюстрацию метода (рисунок 1). Предположим, каким-либо методом определено начальное приближение к корню. В точке x0 вычислим левую часть решаемого уравнения f0 = f (x0), а также производную в этой точке f ¢ (x0) = tg a. Следующее приближение к корню найдем в точке x1, где касательная к функции f (x), проведенная из точки (x0, f0) пересекает ось абсцисс. Затем считаем точку х1 в качестве начальной и продолжаем итерационный процесс. Из рисунка 1 видно, что таким способом можно приближаться к корню х*. При этом расстояние между очередным xk+1 и предыдущим xk приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие
|xk+1 – xk| < e ,
где e - допустимая погрешность вычисления корня.
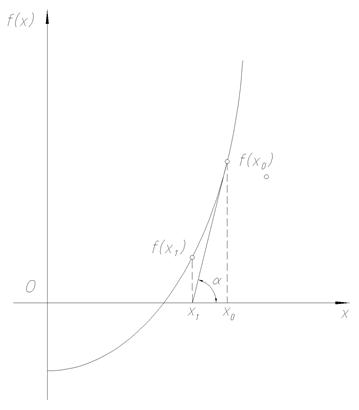
Рисунок 1 – Метод Ньютона
Из геометрических соотношений рисунка 1 получим основную формулу метода Ньютона
x1 = x0 – f (x0) / f ¢ (x0) .
В общем виде для k-го шага итерационного процесса последнее соотношение принимает вид
xk+1 = xk – f (xk) / f ¢ (xk) .