Рассматриваемый метод так же, как и метод деления отрезка пополам, предназначен для уточнения корня на интервале [a, b], на концах которого левая часть уравнения f(x) = 0 принимает разные знаки. Значение начала интервала а вводится с клавиатуры.
Очередное приближение теперь в отличие от метода деления отрезка пополам берем не в середине отрезка, а в точке х1, где пересекает ось абсцисс прямая линия, проведенная через точки f(a) и f(b) (рисунок 1).
В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [a, x1] или [x1, b], на концах которого функция f(x) принимает значения с разными знаками.
Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной точностиe
|xn – xn-1| < e
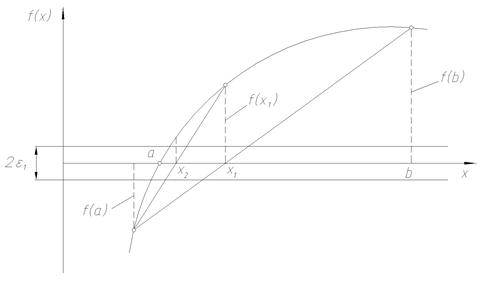
Рисунок 1 – Метод хорд
Уравнение прямой линии, проходящей через точки fa = f(a) и fb = f(b), запишем в общем виде
y(x) = kx + c .
Коэффициенты k и c уравнения этой прямой определим из условий
fa = ka + c ,
fb = kb + c .
Вычитая левые и правые части последних соотношений, получим
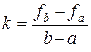, c = fa – ka .
Точку пересечения прямой y(x) с осью абсцисс получим, приравнивая y(x) нулю
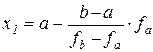(1)
или
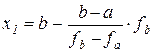. (2)
