Методические указания

7.1 Ввод и вывод массива, а также операции над матрицами оформить в виде функций, не возвращающих значение.

7.2 При вводе, выводе и обработке матриц использовать указатели на массивы

Варианты заданий

1. Даны квадратные матрицы А и В порядка n. Получить матрицу С = А×В - В×А.

2. Дана квадратная матрица А порядка n. Получить матрицу А×В+B, где элементы матрицы В вычисляются по формуле:

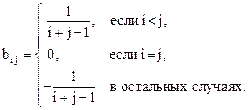
3. Даны квадратные матрицы А и В порядка n. Получить матрицу С = А^Т - В^ТA, где А^Т и В^Т – транспонированные матрицы.

4. Даны квадратные матрицы А и В порядка n. Получить произведение А×В^Т

5. Даны квадратные матрицы А и В порядка n. Получить матрицу А² + В².

6. Даны квадратные матрицы А, В и С порядка n. Получить матрицу (А+В)×С.

7. Дана квадратная матрица А порядка n. Получить матрицу А^Т×В^Т, где А^Т и В^Т – транспонированные матрицы, а элементы матрицы В вычисляются по формуле:

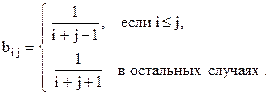
8. Даны квадратные матрицы А и В порядка n. Получить матрицу А×(В – Е) + С, где Е – единичная матрица порядка n, а элементы матрицы С вычисляются по формуле:

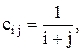i, j = 1, 2, …, n.

9. Дана матрицы А и В размера m´n . Получить матрицу А^Т + В^Т, где А^Т и В^Т – транспонированные матрицы.

10. Дана квадратная матрица А порядка m. Получить матрицы 0.5×(A + A^T) и 0.5×(А – А^Т), где А^Т – транспонированная матрица.