Ввод матрицы обычно задается по строкам с помощью двух циклов. При использовании указателей это будет выглядеть следующим образом:
/* Ввод матрицы по строкам */
void input_matr (float *matr, int n, int m)
{
int i, j;
for (i = 0; i < n; i++)
{
cout<<“\nвведите элементы “<<i + 1<<”-й строки: “ ;
for(j = 0; j < m; j++)
cin>>matr[ i*m + j];
}
}
Вывод матрицы организуется построчно, как и ввод, с помощью двух циклов. При использовании указателей это будет выглядеть следующим образом:
/* Вывод матрицы по строкам *.
void out_matr(float *matr, int n, int m)
{
int i, j;
for (i = 0; i < n; i++)
{
for (j = 0; j < m; j++)
cout<<(matr[i*m + j]<<” “;
cout<<endl;
}
cout<<endl;
}
Операции с константами сводятся к сложению или вычитанию элементов матрицы aij с константой, например х, или умножению aij*х или делению aij/х на константу.
Транспонированной матрицей называется матрица, у которой столбцы и строки меняются местами, т. е. из матрицы размера m´n получатся матрица размером n´m. Например, для матрицы А размером 3´4это:
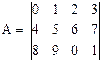
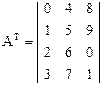
Нетрудно заметить, что транспонирование матрицы реализуется с помощью соотношения 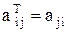 .
.
Произведением двух квадратных матриц А и В является третья матрица С, элементы которой вычисляются по формуле:
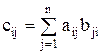 .
.
Таким образом, элемент сij матрицы С = А×В есть сумма произведений элементов i-й строки матрицы А на соответствующие элементы i-го столбца матрицы В.
