1) Даны отрезки a, b, c и d. Для каждой тройки этих отрезков, из которых можно построить треугольник, вычислить площадь этого треугольника и вывести на экран.
2) Даны действительные числа x, y, z. Вычислить выражение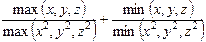 
.
3) Даны длины a, b и c сторон некоторого треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. (Замечание: длина медианы проведенной к стороне a, равна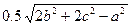 
.)
4) Даны действительные числа a, b, c. Получить
.
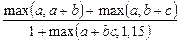5) Даны действительные числа s, t. Получить h(s, t) + max(h2(s – t, st), h4(s – t, s + t)) + h(1, 1) ,
где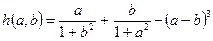 
.
6) Даны действительные числа a0, a1, a2, a3. Получить для x = 1, 2, 3, 4 значения p(x +1) – p(x), где
p(y) = a3y3 + a2y2 + a1y + a0.
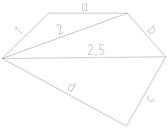
7) Даны действительные числа a, b, c, d. Найти площадь пятиугольника, изображенного на рисунке. (Определить функцию вычисления площади треугольника по трем его сторонам.)
8) Дано действительное число y. Получить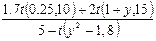 
, где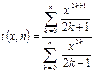 
.
9) Для вещественного числа a > 0 вычислить величину
.
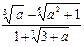Корни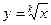 
вычислять с точностью e = 0.0001 по следующей итерационной формуле:
,
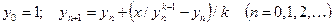приняв за ответ приближение yn+1, для которого |yn+1 – yn| < e.
10) Даны действительные числа a, b, c. Получить
.
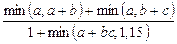