Теория подобия - это теория, дающая возможность установить наличие подобия или позволяющая разработать способы получения его.
Основной характеристикой подобных объектов являются критерии подобия, с помощью которых устанавливаются закономерности взаимооднозначного соответствия модели и оригинала.
Критерии подобия - это идентичные по форме алгебраической записи и равные численно для подобных объектов безразмерные степенные комплексы определенных групп параметров, характеризующих эти объекты.
Пусть объект описывается уравнением F(p1p2…pn) = 0.
F – функциональная зависимость между параметрами объекта, pi – параметры объекта.
Данное уравнение – полное физическое уравнение, характеризующее объект во всех ситуациях.
В частных случаях некоторые параметры при некоторых условиях остаются постоянными, тогда данное уравнение будет называться неполным физическим уравнением.
Пусть Pj = const = k1 , тогда F(p1, p2,…pk, pk+1,… pn) = 0.
{ p1 …pn} – все параметры
{ p1 …pk} – группа независимых параметров
{ pk+1 …pn} - группа зависимых параметров
n – общее количество всех параметров;
k – количество независимых параметров, которое определяется как ранг матрицы, состоящей из степеней единиц измерения параметров;
(n-k) - количество зависимых параметров, количество критериев подобия для данной системы 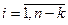 .
.
Критерии подобия могут быть установлены при известном и неизвестном математическом описании объекта.