KV-диаграмма может быть представлена во многих вариантах. Для того чтобы избежать длинных разделений, целесообразно остановится на одной версии. Пример в рисунке 1.1.5.1 описывает нахождение минимальных дизъюнктивных нормальных форм. При этом речь идет о KV-диаграмме для четырех входных переменных с A = 23 (самый высокий по значению бит).
KV-диаграмма содержит все минтермы. Для дальнейшего упрощения их можно заменять соответствующими двоичными числами (рисунок 1.1.5.2).
Для применения KV-диаграммы минтермы считываются с таблицы значений и переносятся в KV-диаграмму.
В качестве примера может подойти рисунок 1.1.5.2:
| Рисунок 1.1.5.1 KV-диаграмма для четырех входных переменных
| |
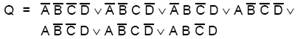
Q=0 v 2 v 5 v 8 v 9 v 10 v 13
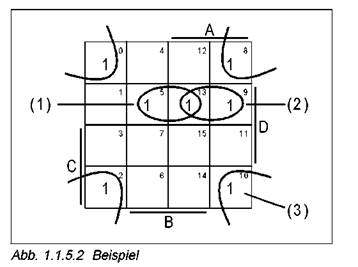
Затем объединяются соседние поля, занятые «1», таким образом, что данное соединение содержит как можно больше единиц. При этом могут быть объединены поля 2n(n = натуральное число). На KV-диаграмме на рисунке 1.1.5.2 показаны три возможных объединения.
Выражения алгебры переключательных схем сохраняются, в то время как все поля общих переменных величин объединены в логическую операцию «И».
Выражения для объединения выглядят следующим образом:
Следовательно, минимальная переключательная функция выглядит следующим образом:
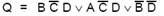
По сравнению с полной дизъюнктивной нормальной формой она содержит только восемь переменных величин.
