 
|
| Рис. 61. Схема дифференцирующего усилителя
|
Пусть ОУ идеальный: 
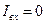. Тогда уравнение Кирхгофа для точки А запишется в следующем виде:
| (116)
|
| Раскрыв токи, получим:
|
|
| (117)
|
| Определим потенциал точки А:
|
|
| (118)
|
| С учетом этого:
|
|
 ,
| (119)
|
| Откуда выразим выходное напряжение:
|
|
| (120)
|
где  – коэффициент передачи дифференцирующего усилителя.
|
При наличии на входе схемы прямоугольных импульсов, как это показано на осциллограмме:
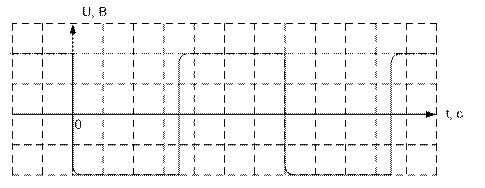
На выходе схемы получим сигналы следующего вида:
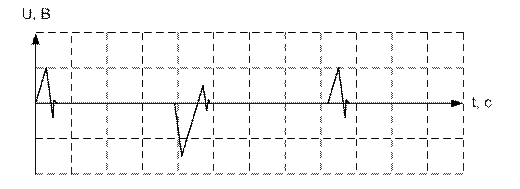
Так как дифференциал – это скорость изменения, то там где входной сигнал меняется, там всплеск, там, где сигнал не меняется, там нет всплеска.Чем меньше крутизна фронта или спада, тем меньше амплитуда на выходе дифференцирующего усилителя (так как скорость изменения сигнала меньше).На практике рассмотренная схема не применяется, потому что она склонна к самовозбуждению и имеет низкую помехоустойчивость, что поясняется рис. 62.
|
| Рис. 62. К пояснению неустойчивости дифференцирующего усилителя
|
В районе частоты 
происходит пересечение частотной характеристики схемы с обратной связью с АЧХ скорректированного ОУ. И в районе частоты максимальное изменение АЧХ будет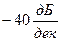 
в этом случае возможен фазовый сдвиг примерно 
, поэтому схема начнет самовозбуждаться. Для исключения самовозбуждения в схему вводят частотную коррекцию (обозначено пунктиром на рис. 84).
Введением коррекции исключается пересечение характеристик на участке со спадом .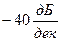
