Дискретное преобразование Хартли имеет вид [3]:
- прямое преобразование
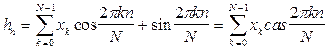(6.5)
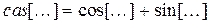
- обратное преобразование
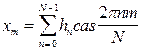
Матрица ядра преобразования Хартли может быть записана как:
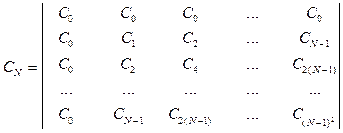
где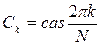 
, причем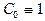 
Матрица ядра преобразования обладает следующими свойствами:
1) цикличностью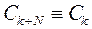 
; 
;
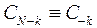2) отсутствием мультипликативности, т.е.: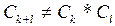 
3) симметричностью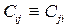 
Отсюда следует, что обратная матрица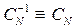 
, поскольку 
.
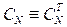4) из свойства цикличности следует, что в матрице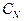 
имеется лишь N различных между собой коэффициентов 
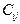из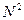 
Для N =2, N=4 и N = 8 матрицы ядра преобразования будут иметь вид:
N =2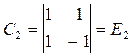 
N=4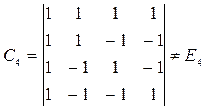 
N = 8 
Таким образом, в отличии от матрицы ДЭФ, матрица ядра преобразования Хартли содержит коэффициенты, большие единицы.
