Со сложением двоичных чисел все понятно. Как же осуществить на микросхемах-сумматорах опрации вычитания двоичных чисел? Допустим необходимо выполнить вычитание: 11 - 5 = 6. В двоичных эквивалентах произведем операцию сложения числа 1011 (число 11) и обратный код числа 5, равный 1010 (прямой код 0101). Итак:
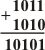
Если отбросить единицу в старшем (пятом) разряде, то получится код 0101, который соответствует числу 5. Но это не число 6. Значит к результату необходимо прибавить единицу. Кстати, операция увеличения какого-либо числа на единицу называется инкрементом, уменьшения на единицу - декрементом. На рисунке 2 показана схема четырехразрядного вычитателя.
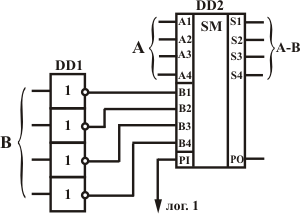
Рис. 2 - 4-х разрядное усройство вычитания
Инверторы микросхемы DD1 формируют обратный код числа В. Число А поступает на входы А1-А4 сумматора DD2, обратный код числа В - на входы В1-В4 сумматора. На вход переноса Р0 подан уровень лог. 1, что обеспечивает прибавление к результату сложения единицы (т. е. инкремент результата). На выходах S1-S4 сумматора в итоге получается разность между числами А и В.