Поступательное движение со скоростью υ совершает груз массой массой m ( рис. ,
13, а ).
Кинетическая энергия этой массы при поступательном движении
А = (mυ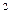 
) /2 ( 48 )
Эта же энергия после приведения к валу двигателя
А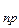 
= ( J" 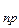ω 
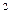
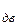) /2 ( 49 )
На основании принципа энергетического баланса
А = А 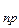( 50 )
Поскольку, в соответствии с уравнением ( 50 ), в уравнениях ( 48 ) и ( 49 ) одинако-
вы левые части, приравняем их правые части:
(m*υ 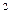) /2 = ( J" 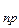ω 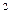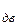) /2. ( 51 )
Предварительно сократив обе части равенства ( 51 ) на 2, найдем значение приве-
денного момента инерции поступательно движущейся массы:
J" 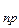= (m*υ 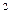) / ω 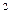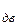( 52 )
Как следует из уравнения ( 52 ), этот момент тем больше, чем больше масса груза
m и её скорость υ, и чем меньше скорость двигателя ω .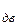
Пример №12.
В электроприводе лебедки масса груза m = 3000 кг, скорость перемещения груза
υ = 0,75 м / с, угловая скорость вала двигателя ω 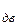= 104,5 с 
.
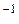Найти приведенный момент инерции, создаваемый грузом.
Решение
Приведенный момент инерции, создаваемый грузом.
J" 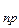= (m*υ 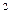) / ω 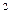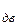= ( 3000*0,75 
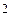) / 104,5 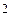= 0,0867 кгм .
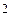