Выведем формулу динамического момента и ее помощью выясним его роль.
Пусть абстрактное тело с моментом инерции Ĵ вращается с угловой скоростью ω.
Для вывода формулы динамического момента этого тела используем 3 формулы, известные из курса физики:
1. кинетическая энергия вращающегося тела
A = (J *ω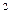 
) / 2 ( 29 )
где: J - приведенный ( к оси вращения ) момент инерции тела;
2. мощность, выраженная через работу
Р = А / t ( 30 )
где: А - работа, выполненная за время t ;
3. мощность тела при вращательном движении
P = Mω ( 31 )
где: М – вращающий момент тела.
Последние 2 формулы запишем применительно к динамическому режиму:
4. мощность, выраженная через работу
Р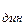 
= dА / dt ( 32 )
5. мощность тела при вращательном движении
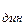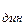Р = М ω ( 33 ).
В формулах ( 4 ) и ( 5 ) одинаковы левые части, поэтому приравняем правые части
dА / dt = М 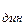ω,
откуда
М 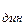= ( dА / dt ) / ω = d [ ( J ω 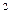)/2 ] / (ω dt)=
= ( J /2 )2ω( dω / ωdt) = J dω / dt ( 34 )
