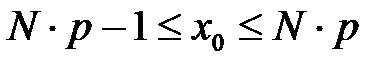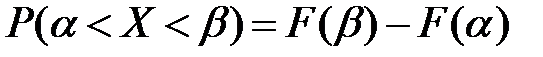или 
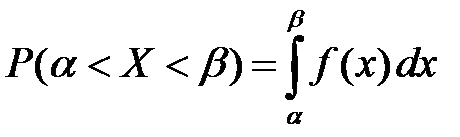
(по определению и свойствам функции F(x) и f(x)).
Если НСВ Х распределена по нормальному закону Х~N(a;σ), вероятность попадания Х в интервал (α;β) вычисляется по формуле
где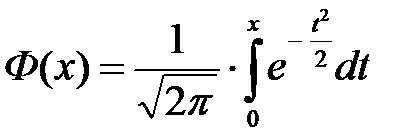 
– функция Лапласа (значения табулированы)
Свойства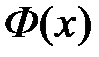 
:
а)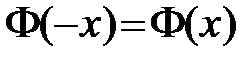 
- функция Лапласа нечётная. б) 
; в)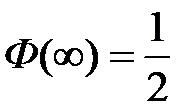 
Пример. СВ Х распределена по нормальному закону с параметрами a=2; σ=4: Х~N(-2;4).Найти вероятность того, что СВХ попадёт в промежуток: а)(0;3),б) (4; ∞), в) (-∞;1).
Решение. а) Р(0<X<3)=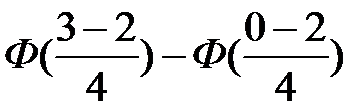 
=Φ(0,25)Φ(0,5)=Φ(0,25)+Φ(0,5) = 0,0987+0,1915=0,29;
б) Р(Х>4) = Р(4<X<∞)=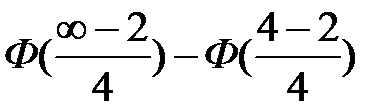 
= Φ(∞) - Φ(0,5)= 0,5-0,1915=0,31;
в) Р(X<1)=Р(-∞<X<3)= 
=Φ(0,25)+Φ(∞)=0,0987+0,5=0,60
Иногда для решения лингвистической задачи необязательно находить вероятности появления данного события 0,1,2,…N раз, а достаточно указать наивероятнейшее число появления этого события х0, которое определяется по формуле 
