Реальные распределения случайных лингвистических единиц не всегда хорошо описываются нормальным законом, обладая правосторонней асимметрией. В связи с этим делаются попытки моделировать эти эмпирические распределения. С этой точки зрения наибольший интерес представляет логарифмически нормальное (логнормальное) распределение. В этом случае нормально распределена не сама СВХ, а её логарифм. Функция плотности вероятности логнормального распределения имеет вид
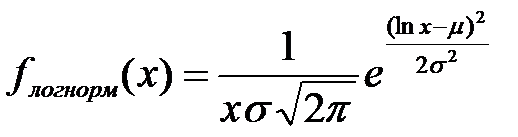 , где
, где 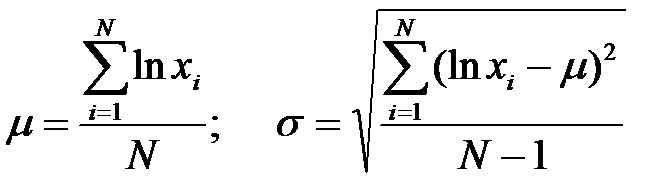 .
.
Функция плотности вероятности логнормального распределения характеризуется островершинностью, и имеет правостороннюю (положительную) скошенность.
Г. Хердан («Квантитативная лингвистика», Лондон, 1964г.) использует логнормальное распределение для математической экспликации вероятностного построения словаря языка и его реализации в тексте. По его мнению, логнормальность словаря и текста отражает присущий естественному языку принцип оптимального кодирования информации.