Дискретная случайная величина Х распределена по закону Пуассона, если она может принимать значения 0, 1, 2, …, n
с вероятностями, которые находятся по формуле Пуассона:
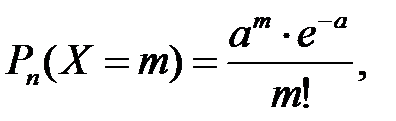где 
Пример. Вероятность появления опечатки на каждой странице текта, содержащего 200 страниц, равна 0,01. Определить:
а) вероятность появления трёх опечаток в тексте;
б) математическое ожидание М(Х) и дисперсию D(X) СВ Х= «количество опечаток в тексте».
Решение. Так как опечатка – редкое событие (р=0,01), то воспользуемся формулой Пуассона для нахождения вероятностей редких событий: 
где р=0,01, n=200, а= n р=0,01 200=2.
Тогда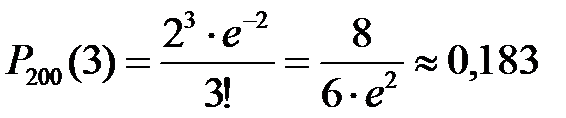 
б) Случайная величина Х – «количество опечаток в тексте» распределена по закону Пуассона, для которого М(Х)=D(X)=а=0,2.
