Дискретная случайная величина Х распределена по биномиальному закону, если она может принимать значения 0, 1, 2, …, n
с вероятностями, которые находятся по формуле Бернулли:
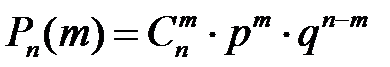; где 
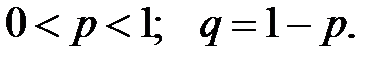
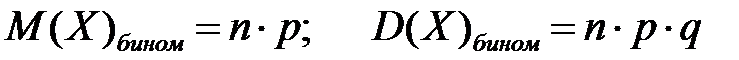
Пример. Пусть производится произвольное извлечение трех словоформ из научно-технического текста. Считая, что вероятность употребления существительного в научно-техническом тексте равна 0,4, для СВ Х ‑ «число выбраных существительных», найти математическое ожидание М(Х) и дисперсию D(Х).
Решение. СВ Х распределена по биномиальному закону, так как испытания являются независимыми, а вероятность появления существительного в каждом из трёх испытаний постоянна.
Здесь n=3, р=0,4, q=1-р=0,6. Тогда М(Х)=n 
р=3 
0,4=1,2; D(Х)=n р q= 3 0,4 0,6=0,72.
Биномиальное распределение СВ используется при описании употребления фонем, графем и их классов, а так же при описании грамматических категорий, при условии, что n – количество испытаний и m - число появлений события А, невелико. В конкретных лингвистических задачах это условие не всегда соблюдается. Например, вероятность появления словоформы ветер в большом тексте мала. Для описания редких лингвистических событий используется распределение Пуассона.
