Определение 1 (устойчивости по Ляпунову) (запись в кванторах).

Фиксированное решение 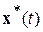системы (1.2.1) устойчиво по Ляпунову при 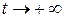, если:

.■

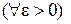
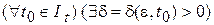
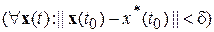
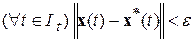Замечание. Убедитесь в экономности этой записи по сравнению с формулировкой определения 1! ■

Определение 2 (асимптотической устойчивости по Ляпунову). Решение 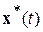системы (1.2.1) называется асимптотически устойчивым по Ляпунову при 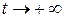, если оно:

а) устойчиво по Ляпунову при 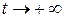(в смысле определения 1);

б) 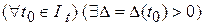такое, что все решения 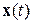системы (1.2.1) удовлетворяющие неравенству

,

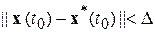обладают предельным свойством вида

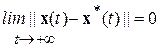.■ (1.2.6)

Решение 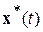, удовлетворяющее условию (1.2.6), называется аттрактивным решением (аттрактором), причем аттрактор не обязательно является устойчивым по Ляпунову (т. е. условие (б) выполняется независимо от условия (а)), само свойство (б) называется свойством притяжения (свойством аттрактивности), а Δ – окрестность (открытый шар радиуса Δ) называется областью притяжения (областью аттрактивности) решения ).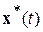