Пусть система из n материальных точек имеет s степеней свободы. В случае голономных, нестационарных связей радиус- вектор ri М i q1 , q2 … qs и времени
ri = ri (q1 , q2 … qs , t ). (17-20)
Обобщенные координаты также являются функциями времени. Поэтому
u i =dri /dt= + ¶ ri /¶ t. (17-21)
В случае стационарных связей
. u i =. (17-22)
Поэтому кинетическая энергия T=
Находя частные производные кинетической энергии по обобщенной координате qj и обобщенной скорости j
( ) - Qj (j=1,2….s). (17-23)
Здесь Qj - обобщенная сила, сопряженная с обобщенной координатой, равная
Qj = . (17-24)
Эти уравнения называются уравнениями Лагранжа второго рода .
Интегрируя эти уравнения и определяя пот начальным условиям постоянные интегрирования, получим s уравнений движения механической системы в обобщенных координатах.
Эти уравнения широко используются при изучении динамики механических систем.
Литература:
1. Яблонский А.А., Никифорова В.М. Курс теоретической механика. Высшая школа.Ч.1., Ч.2.М. 1977, с. 368, с. 430.
Содержание.
1. Введение…………………………………………………………………..стр.4
1.1. Основные понятия статики……………………………………..……………..4
1.2. Аксиомы статики…………………………………………………..………….5
1.3. Несвободное твердое тело. Связи………………………………….…………6
Глава 2. Система сходящихся сил………………………………………..7
2.1. Многоугольник сил. Условия равновесия сходящихся сил……….…….….7
2.2. Теорема о равновесии трех непараллельных сил……………..…………….10
2.3. Проекция силы на оси декартовых координат……………………………..11
Глава 3. Теория пар сил………………………………………………………….13
3.1. . Сложение двух параллельных сил………………………………..……….13
3.2. Пара сил. Момент пары сил………………………………….…………...14
3.3. Теорема об условии эквивалентности пар сил, лежащих в одной
плоскости……………………………………………………………………….15
3.4. Теорема об условии эквивалентности пар сил в пространстве………..16
3.5. Сложение пар сил. Условия равновесия пар сил…………….17
Глава 4..Момент силы относительно точки и относительно оси…………..20
4.1. Момент силы относительно точки как векторное
произведение………………….…………………………………………..20
4.2. Момент силы относительно оси………………………………………...21
4.3.Зависимость между моментами силы относительно точки
и оси, проходящей через эту точку…………………………..……………22
4.4. Аналитические выражения моментов силы относительно
координатных осей………………………………………………………..22
4.5.Момент силы и главный момент системы сил, лежащих в
одной плоскости………………………………………………………….23
Глава 5.Система сил, расположенных произвольно.
5.1. Приведение силы к заданному центру………………………………….24
5.2. Вычисление главного вектора и главного момента системы сил,
произвольно расположенных на плоскости……………………………25
5.3. Уравнения равновесия системы сил, произвольно
расположенных на плоскости…………………………………………..26
5.4. Сложение параллельных сил на плоскости.
Уравнения равновесия параллельных сил……………………………….26
5.5. Рычаг. Устойчивость при опрокидывании. Коэффициент
устойчивости………………………………………………………………29
5.6. Сцепление и трение скольжения………………………………………..31
5.7. Силы произвольно расположенные в пространстве…………………..33
5.8. Уравнения равновесия сил, произвольно расположенных
в пространстве……………………………………………………………..34
5.9. Приведение произвольной системы сил к двум скрещи-
вающимся силам или силовому винту (динаме)……….……………..37
5.10. Несвободное твердое тело с одной и с двумя закрепленными
точками. Определение реакций………………………………………..40
Глава 6. Центр тяжести
6.1.Последовательное сложение параллельных сил. ……………………….45
6.2. Формулы радиуса- вектора и координат центра параллельных
сил…………………………………………………………………………..46
6.3. Центр тяжести твердого тела, плоской фигуры………………………..47
6.4. Центр тяжести линии…………………………………………………….48
6.5 Вспомогательные теоремы………………………………………………..49
К И Н Е М А Т И К А
Глава 7. Кинематические способы задания движения точки.
7.1. Естественный способ задания движения точки……………………….50
7.2. Векторный способ задания движения точки…………………………..50
7.3. Координатный способ задания движения точки.
Уравнение движения точки в декартовых координатах……………….51
7.4. Скорость точки. Определение скорости при задании ее движения
векторным способом. Вектор скорости…………………………………53
7.5. Определение скорости точки при задании ее движения
координатным способом………………………………………………...56
7.6. Ускорение точки. Определение ускорения при задании движения
векторным способом. Вектор ускорения………………………………56
7.7. Определение ускорения точки при задании ее движения коорди-
натным способом. Проекции ускорения……………………………….57
7 .8. Естественные координатные оси. Вектор кривизны…………………59
7.9. Определение ускорения точки при задании движения естественным
способом………………………………………………………………….60
7.10. Классификация движений точки по ускорениям ее движения……62
7.11. Графики движения, пути, скорости и касательного
ускорения……………………………………………………………….66
Глава 8. Простейшие движения твердого тела.
8.1. Поступательное движение………………………………………………68
8.2 Вращательное движение…………………………………..…………….68
8.3 Плоское движение плоского тела……………………………………....70
8.4. План скоростей…………………………………………………………..73
8.5. Мгновенный центр скоростей………………………………………….74
8.6. Ускорения точек плоской фигуры……………………………………..78
8.7. Мгновенный центр ускорения………………………………………….82
8.8. Сложное движение точки………………………………………………88
Глава 9. Общий случай движения твердого тела.
9.1. Разложение движения свободного тела на поступательное вместе
с полюсом и сферическое движение вокруг полюса…………………..90
Глава 10. ДИНАМИКА.
10.1. Введение………………………………………………………………..91
10.2. Динамика свободной материальной точки………………………….92
10.3 Свободное падение тела без учета сопротивления воздуха………...94
10.4. Движение тела , брошенного под углом к горизонту без
учета сопротивления воздуха………………………………………94
10.5. Колебательное движение материальной точки.
Свободные колебания…………………………………………………96
10.6. Вынужденные колебания материальной точки………………….….101
Глава 11. Динамика несвободной точки.
Связи и динамическая реакция связей…………………………..108
11.2 Дифференциальное уравнение движения материальной точки
(МТ) по заданной неподвижной поверхности и плоской кривой…111
11.3. Математический маятник и его малые колебания………………….114
Глава 12. Динамика относительного движения материальной
точки (МТ).
12.1. Дифф. уравнения. Переносная и кориолисова сила инерции.
Принцип относительности…………………………………………..115
12.2. Относительный покой. Сила тяжести……………………………….118
12.3. Отклонение падающих тел…………………………………………..119
Глава 13. Система материальных точек. Моменты инерции
твердого тела.
13.1. Силы, действующие на точки механической системы……………121
13.2. Моменты инерции твердого тела…………………………………...123
Глава 14. Движение центра масс.
14.1. Теорема о движении центра масс механической
системы…………………………………………………………125
14.2. Изменение количества движения материальной точки и
механической системы. Импульс силы…………………………….128
14.3. Момент количества движения материальной точки (МТ)
и его изменение…………………………………………………..…..130
14.5. Работа. Две меры механического движения………………………..133
14.6. Элементарная работа. Теоремы о работе силы………………………134
14.7. Работа силы тяжести. Силы упругости………………………………137
14.8. Теорема об изменении кинетической энергии
материальной точки…………………………………………………….138
14.9. Работа сил, приложенных к твердому телу………………………….140
14.10. Сопротивление при качении………………………………………..141
14.11. Кинетическая энергия механической системы
(теорема Кенига)……………………………………………………………..142
14.12. Механический коэффициент полезного действия…………………143
14.13. Потенциальное силовое поле………………………………………...144
14.14. Закон сохранения механической энергии…………………………..146
Глава 15. Динамика поступательного и вращательного движений
твердого тела.
15.1. Дифференциальное уравнение поступательного движения
твердого тела……………………………………………………………..147
15.2. Дифференциальное уравнение вращения твердого
тела вокруг неподвижной оси…………………………………………147
15.3 Динамика сферического и свободного движений
твердого тела……………………………………………………………..149
15.4 Понятие о гироскопе……………………………………………………151
Глава 16. Теория удара.
16.1 Явление удара……………………………………………………………153
16.2. Удар шара о неподвижную поверхность……………………………...155
16.3. Прямой центральный удар двух тел…………………………………..157
16.4. Теорема Карно…………………………………………………………..159
16.5. Теорема об изменении кинетического момента механической
системы при ударе……………………………………………………….160
Глава 17. Принцип возможных перемещений.
17.1. Обобщенные координаты и число степеней свободы………………...161
17.2. Возможные перемещения механической системы……………………..161
17.3. Общее уравнение динамики……………………………………………..163
17.4.Общее уравнение динамики в обобщенных силах……………………..164
17.5. Понятие об устойчивости состояния покоя системы
с одной степенью свободы в консервативном поле……………………167
17.6. Уравнения Лагранжа 2-го рода…………………………………………..168.
Содержание………………………………………………………………………169.
[1] Жирными буквами обозначены векторы.
[2] Док-во см. [1].
[3] Док-во см. [1]
Тема 3 . Методи поиска решений творческих инженерных задач
+ ¶ri /¶ t. (17-21)
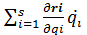. (17-22)
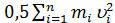является тоже функцией обобщенных координат и времени.
j и делая соответствующие преобразования, получим уравнение
( 
) - 
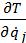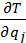= Qj (j=1,2….s). (17-23)
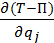. (17-24)