Линейное преобразование называется самосопряженным, если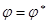 
.
Свойство 8.7. Собственные числа самосопряженного преобразования – вещественны.
Доказательство. Пусть x –собственный вектор самосопряженного преобразования 
(т.е. 
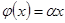). Из равенств 
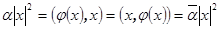выводим 
, то есть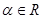 
.
Следствие 8.2. Для самосопряженного линейного преобразования евклидова пространства существует ортонормированный базис из собственных векторов.
Доказательство. Самосопряженное преобразование является нормальным, и значит, существует ортонормированный базис, в котором матрица линейного преобразования имеет блочно диагональный вид. Поскольку все собственные числа вещественные, то все блоки первого порядка.
