Однозначное отображение 
линейного пространства V над числовым полем P в себя называется линейным преобразованием, если оно сохраняет линейность, то есть 
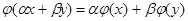для любых 
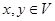и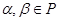 
.
Линейное преобразование полностью определяется своими значениями на базисных векторах. Действительно, пусть 
базис V. Вектор x разложим по базису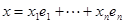 
, где 
- координаты вектора x. По свойству линейного преобразования имеем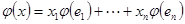 
. Перейдем в последнем равенстве от равенства векторов к равенству их координат 
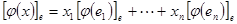, которое можно записать используя матричное умножение следующим образом 
. Матрица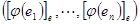 
называется матрицей линейного преобразования и обозначается 
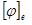. Матрица линейного преобразования связывает координаты образа с координатами исходного вектора 
.
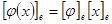