Рассмотрим несовместную систему линейных уравнений Ax=b. Псевдорешением системы линейных уравнений называется вектор x, на котором достигается минимум нормы невязки |Ax-b|. Задача построения псевдорешения возникает при подборе параметров физических процессов. Левая часть системы уравнений определяется конкретным видом зависимости от параметров, а правая – конкретными измерениями. Поскольку каждое измерение производится с некоторой точностью, то обычно их проводят с избытком. В результате получается несовместная система линейных уравнений, а задача подбора параметров сводится к построению псевдорешения. Сам способ перехода от задачи решения системы линейных уравнений к нахождению минимума длины невязки называется метод наименьших квадратов. Такое название связано с тем, что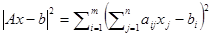 
.
Обозначим через W линейную оболочку столбцов матрицы A. Задача построения псевдорешения эквивалентна задаче определения расстояния от b до W,а точнее к определению проекции b на W. Коэффициенты разложения проекции по столбцам матрицы A являются решениями системы уравнений 
. Тем самым, задача построения псевдорешения свелась к решению системы линейных уравнений.
Если исходная система имела решение, то оно является также псевдорешением. Необходимым и достаточным условием единственности псевдорешения является условие линейной независимости столбцов матрицы A.
