Определение 2.1. Векторы называются ортогональными, если их скалярное произведение равно 0.
Теорема 2.1 (Пифагора). Пусть векторы x и y ортогональны, тогда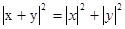 
.
Доказательство.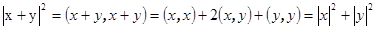 
, т.к. 
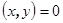в силу ортогональности.
Теорема 2.2 (неравенство Бесселя). Пусть векторы x и y ортогональны, тогда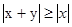 
.
Доказательство. По теореме Пифагора 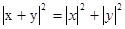. Поскольку 
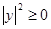, то 
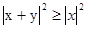, что и требовалось.
Теорема 2.3 (неравенство Коши-Буняковского-Шварца).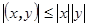 
.
Доказательство. Для любого a справедливо неравенство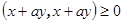 
. Раскроем левую часть 
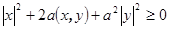. В левой части неравенства записан квадратный трехчлен. Выделим из него полный квадрат 
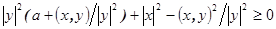. Положив 
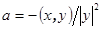получим неравенство 
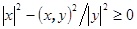из которого вытекает 
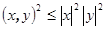. Извлекая квадратный корень, получаем требуемое.
Неравенство Коши-Буняковского-Шварца позволяет ввести угол между векторами, то есть косинус угла равен отношению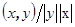 
.
Определение 2.2 Система векторов называется ортогональной, если каждая пара векторов из этой системе ортогональна.
Свойство 2.1. Ортогональная система векторов линейно не зависима.
Доказательство. Пусть 
- ортогональная система векторов и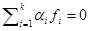 
. Тогда 
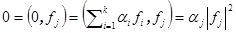. Таким образом 
и система векторов линейно независима.
Свойство 2.2. Матрица Грама ортогональной системы векторов – диагональная.
