Пусть V линейное пространство над полем вещественных чисел. Функция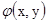 
, ставящая каждой паре векторов в соответствие число, называется скалярным произведением если выполнены аксиомы
1. Линейность по первому аргументу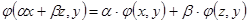 
.
2. Симметричность: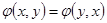 
3. Положительная определенность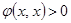 
при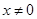 
.
Пространство над полем вещественных чисел, в котором введено скалярное произведение называется евклидовым.
Величина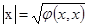 
называется длиной вектора.
Пусть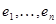 
базис V. Выразим скалярное произведение векторов через координаты векторов. Координаты вектора x в базисе e обозначим через 
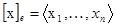. Тогда 
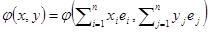. Пользуясь свойством линейности выводим 
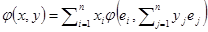. Используя симметричность скалярного произведения и линейности по первому аргументу выводим 
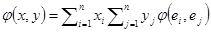. Обозначим через G матрицу Грама базисных векторов, то есть матрицу на пересечении строки i столбца j стоит скалярное произведение i-го и j-го вектора 
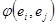. Используя матричные операции умножения получаем 
.
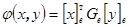