Плоскость – линейное многообразие размерности 2. Плоскость в пространстве задаётся одним уравнением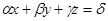 
. Подпространство, соответствующее плоскости, задаётся однородным уравнением 
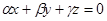. В ортонормированном базисе левая часть уравнения является скалярным произведением вектора 
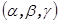и вектора плоскости 
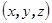. Таким образом, множество векторов плоскости состоит только из тех векторов, которые ортогональны вектору нормали 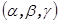. Расстояние от точки 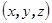до плоскости 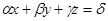равно 
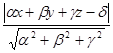. Следовательно, коэффициент 
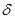определяет удалённость плоскости от начала координат
Прямая в пространстве задаётся системой из двух уравнений (см. раздел Ошибка! Источник ссылки не найден.)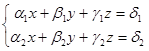 
, причём ранг матрицы, образованной коэффициентами при неизвестных, равен 2. Разберём геометрический смысл коэффициентов. Представив прямую как пересечение двух плоскостей, приходим к выводу, что векторы 
и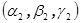 
образуют базис плоскости перпендикулярной исходной прямой.
