Определение 7.12 Сумма подпространств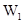 
и 
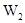называется прямой, если 
. Обозначение прямой суммы 
.
Теорема 7.7. Пусть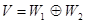 
. Тогда любой вектор 
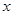из V единственным образом представляется в виде суммы векторов из подпространств 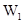и 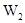, x=y+z. Вектор y называется проекцией x на 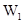параллельно 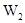, а вектор z называется проекцией x на 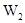параллельно .
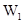Доказательство. Допустим, найдётся вектор 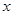, который раскладывается в сумму векторов из подпространств 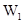и 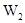не единственным образом. Пусть 
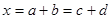, где 
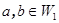и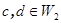 
. Тогда справедливо равенство 
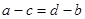, в левой части которого стоит вектор из 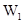, а в правой – вектор из 
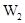. Поскольку пересечение этих подпространств состоит только из нулевого вектора, то 
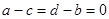, и, значит, a=c, b=d.
Следствие 7.9. Если сумма прямая, то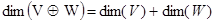 
и базис 
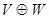получается объединением базисов V и W.
Доказательство. По определению прямой суммы размерность пересечения равна нулю, и, значит, 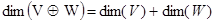(Теорема 7.6). Обозначим через 
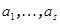базис V, а через 
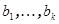- базис W. Покажем линейную независимость системы векторов 
. Допустим, найдутся коэффициенты, что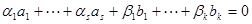 
, тогда справедливо равенство 
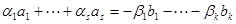. Поскольку в левой части равенства стоит вектор из V, а в правой – вектор из W, то 
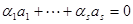и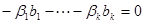 
, и, значит, все коэффициенты равны нулю. Число векторов в линейно независимой системе векторов совпадает с размерностью суммы пространств, следовательно, она является базисом.
