Использование правил блочного произведения матриц позволяет уменьшить общее количество операций, а значит, и время выполнения работы программы. Допустим, требуется умножить квадратные матрицы A и B порядка 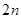 . При перемножении матриц, по формулам, приведённым в определении произведения, потребуется
. При перемножении матриц, по формулам, приведённым в определении произведения, потребуется 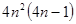 умножений и сложений. Разобьём матрицы A и B на блоки
умножений и сложений. Разобьём матрицы A и B на блоки 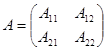
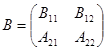 порядка n. Вычисление произведения блочных матриц проведём по формулам Штрассена
порядка n. Вычисление произведения блочных матриц проведём по формулам Штрассена
-
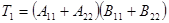 потребуется
потребуется  умножений и сложений
умножений и сложений -
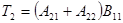 потребуется
потребуется 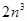 умножений и сложений
умножений и сложений -
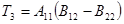 потребуется
потребуется 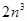 умножений и сложений
умножений и сложений -
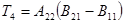 потребуется
потребуется 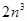 умножений и сложений
умножений и сложений -
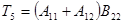 потребуется
потребуется 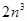 умножений и сложений
умножений и сложений -
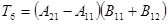 потребуется
потребуется  умножений и сложений
умножений и сложений -
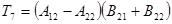 потребуется
потребуется  умножений и сложений
умножений и сложений -
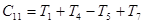 потребуется
потребуется 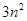 сложений
сложений -
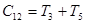 потребуется
потребуется 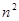 сложений
сложений -
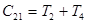 потребуется
потребуется 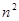 сложений
сложений -
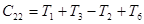 потребуется
потребуется 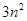 сложений.
сложений.
Всего, для вычисления произведения матриц по формулам Штрассена, потребуется 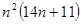 операций сложения и умножения. При выполнении неравенства
операций сложения и умножения. При выполнении неравенства  (n>7) формулы Штрассена приводят к меньшему объёму вычислений. Выигрыш в числе операций будет увеличиваться, если при вычислении произведения матриц (шаги1-7) использовать ту же схему.
(n>7) формулы Штрассена приводят к меньшему объёму вычислений. Выигрыш в числе операций будет увеличиваться, если при вычислении произведения матриц (шаги1-7) использовать ту же схему.
Обозначим через 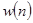 число операций сложения и умножения, используемых при умножении матриц n-го порядка по формулам Штрассена. Справедлива рекуррентная формула
число операций сложения и умножения, используемых при умножении матриц n-го порядка по формулам Штрассена. Справедлива рекуррентная формула 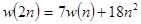 . Положим
. Положим 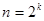 . Тогда
. Тогда 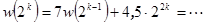
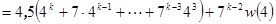 , далее, свернём сумму по формуле суммы членов геометрической прогрессии и заметим
, далее, свернём сумму по формуле суммы членов геометрической прогрессии и заметим 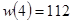 . В результате получим
. В результате получим  . Подставив вместо k его выражение через n (
. Подставив вместо k его выражение через n ( 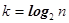 ) получим
) получим 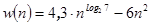 (
( 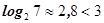 ).
).