Рассмотрим систему линейных уравнений Ax=b, где матрица A невырожденная. Умножим слева это равенство на обратную матрицу, придем к равенству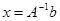 
. Решение системы существует и единственно. Элемент обратной матрицы, расположенный на пересечении строки i и столбца j равен 
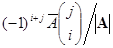. Следовательно, i-ая компонента x равна 
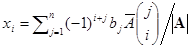. Сумма 
является разложением по столбцу i определителя матрицы, отличающейся от A столбцом i, равным b. Обозначим через 
значение этого определителя. Тогда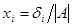 
. Оформим полученные результаты в виде теоремы.
Теорема 6.2 (Правило Крамера). Квадратная система уравнений с невырожденной матрицей имеет единственное решение, компоненты которого находятся по формулам 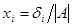, где значение определителя матрицы, отличающейся от A столбцом i, равным b.
