Теорема 5.2 (Бине-Коши). . Пусть A матрица размерами m*n, а B матрица размерами n*m (n больше либо равно n). Справедливо равенство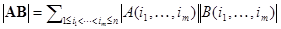 
, где 
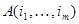- матрица, образованная столбцами матрицы A с номерами 
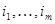, а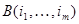 
- матрица, образованная строками матрицы B с номерами .
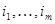Доказательство. Пусть C=AB. По определению определителя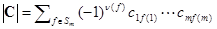 
. Выразим элементы C через элементы A и B, получим 
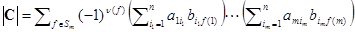. Перемножим все суммы придем к выражению 
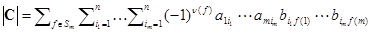. Поменяем порядок суммирования, поставив сумму по подстановкам на последнее место. Вынесем за знак суммы сомножители не зависящие от f получим 
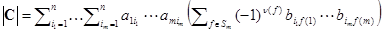. Сумма 
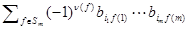есть определитель матрицы 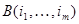, следовательно, 
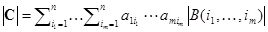. Определитель, содержащий одинаковые строки равен 0, поэтому исключив из последней суммы слагаемые с одинаковыми номерами строк, придем к выражению 
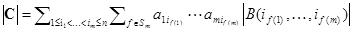. Для упорядочивания строк матрицы 
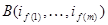потребуется 
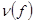подстановок соседних строк (см.Теорема 4.1), следовательно, 
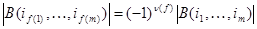и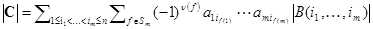 
. Вынесем за знак последней суммы множители не зависящие от f 
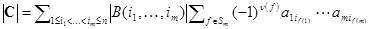. Сумма 
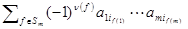есть определитель матрицы 
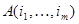, следовательно, 
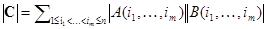, что и требовалось.
Следствие 5.4. Пусть A и B квадратные матрицы порядка n. Тогда определитель произведения равен произведению определителей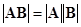 
.
