Рассмотрим многочлен с вещественными коэффициентами 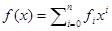. Над полем комплексных чисел он раскладывается на линейные множители. Если a его комплексный корень, то 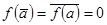, т.е. 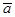то же корень f(x). Таким образом, многочлен f(x) делится на трёхчлен 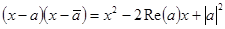с вещественными коэффициентами. Тем самым устанолена
Теорема 2.20. Над полем вещественных чисел многочлен раскладывается в произведение неприводимых многочленов степени 1 и 2. Разложение единственно с точностью до перестановки сомножителей.
. Над полем комплексных чисел он раскладывается на линейные множители. Если a его комплексный корень, то 
, т.е. 
то же корень f(x). Таким образом, многочлен f(x) делится на трёхчлен 
с вещественными коэффициентами. Тем самым устанолена