Обозначим корни уравнения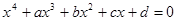 
через 
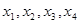. Положим 
, 
, 
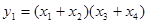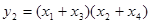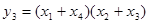. Легко проверить, что перестановка переменных 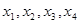приводит лишь к некоторой перестановке 
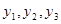и поэтому, элементарные симметрические многочлены от 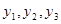являются симметрическими многочленами от 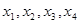. Следовательно, можно написать уравнение третей степени, коэффициенты которого суть многочлены от коэффициентов исходного многочлена, корнями которого являются 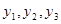. Кубическое уравнение называют кубической резольвентой. После нахождения корней 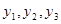, из уравнения 
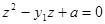( к нему сводится решение системы , 
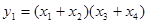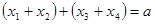) находим 
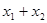, из уравнения 
- 
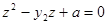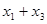, и из уравнения 
- 
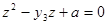. Выразив все корни через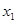 
и подставив выражения в уравнение 
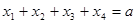найдём все корни исходного уравнения.
