Обозначим корни кубического уравнения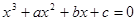 
через 
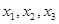. Положим 
и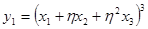 
, 
. Легко проверить, что 
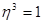и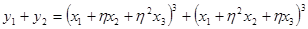 
, 
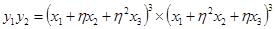- симметрические многочлены от 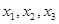. По основной теореме алгебры симметрических многочленов их можно выразить через элементарные симметрические многочлены, значения которых, по формулам Виета, совпадают с точностью до знака с коэффициентами исходного многочлена. Проведя несложные вычисления, получим 
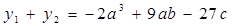и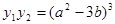 
. По формулам Виета 
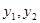- корни квадратного уравнения 
и могут быть вычислены по формулам 
. Таким образом справедливы уравнения 
, 
, 
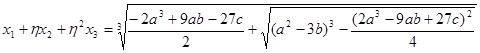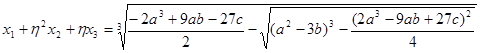. Из этой системы находим корни исходного уравнения.
