Цилиндрическая поверхность получается в том случае, когда прямолинейная образующая при движении пересекает направляющую а и остается параллельной сама себе и указанному направлению S, стремящемуся к бесконечности. Цилиндрическая поверхность является частным случаем конической, когда вершина S удалена в бесконечность.
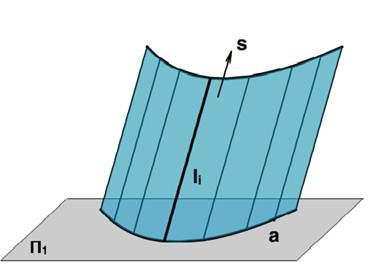
Определитель цилиндрической поверхности может иметь два вида:
Г (а, l), li a, li | | l
Г (a, s), li a, li S .
На рисунке показано задание цилиндрической поверхности и дискретного каркаса образующих.
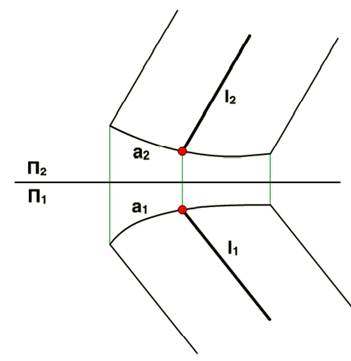
На рисунке показано задание цилиндрической поверхности на ортогональном чертеже.
Если направляющая а является кривой 2-го порядка, то при движении образуется цилиндр 2-го порядка. Если направляющая а – ломаная, то образуется призматическая поверхность, которую можно считать частным случаем цилиндрической поверхности.