В предыдущих пунктах мы рассмотрели случаи пересечения прямой и плоскости при частном расположении пересекающихся фигур. Теперь обратимся к решению одной из главных позиционных задач: нахождение точки пересечения прямой общего положения с плоскостью общего положения.
Построим точку К - точку пересечения прямой общего положения а с плоскостью общего положения b, заданную тремя точками А, В, С.
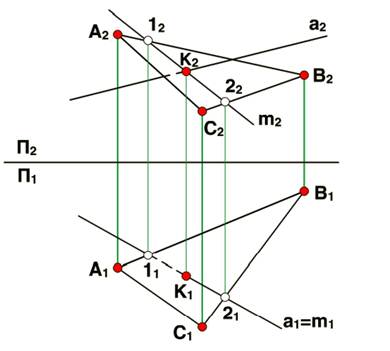
Алгоритм построения точки пересечения:
Например на П1 проведем через заданную прямую а1 вспомогательную горизонтально проецирующую плоскость s1: а s и s П1.
Построим m1 - линию пересечения вспомогательной плоскости s1 с заданной плоскостью b1. Отметим точки 11 и 21 - точки пересечения прямой m1 и отрезков А1В1 и В1С1 соответственно.
Построим фронтальную проекцию прямой m, учитывая принадлежность точек 1 и 2 сторонам треугольника АВС.
Находим точку К2 - точку пересечения прямых m2 и а2: К2=m2 а2.
По линии связи находим первую проекцию точки К - точку К1.
Определяем видимость прямой а с помощью метода конкурирующих точек. На П2, правая часть прямой а2 (относительно точки К2) - видима, а левая часть прямой а2 - невидима. На П1, левая часть прямой а1 (относительно точки К1) - невидима, а правая часть прямой а1 - видима.