Двумя основными позиционными задачами являются:
1. задача на пересечение прямой общего положения с плоскостью общего положения;
2. задача на пересечение двух плоскостей общего положения.
Прежде чем решать эти основные позиционные задачи рассмотрим частные случаи решения задач, т. е. решения позиционных задач при частном расположении пересекающихся фигур.
Рассмотрим построение проекций точки K - точки пересечения прямой а общего положения с фронтально проецирующей плоскостью s.
Плоскость s проецируется на П2 в виде прямой - s2, а на П1 первая проекция плоскости s совпадает с плоскостью П1.
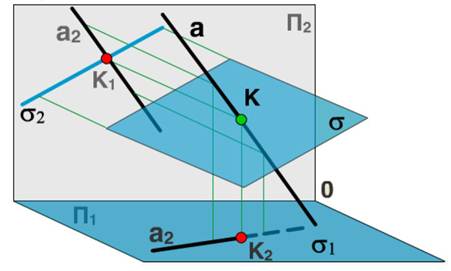
Вторая проекция точки К - К2 является точкой пересечения вырожденной проекции s2 плоскости s и а2 - второй проекции прямой а: а2 s2 = К2. Проекцию К1 находим по принадлежности точки К прямой а: К1 а1.
Дополним рисунок изображением видимых и невидимых участков прямой а, плоскость считаем непрозрачной. Левая полупрямая до точки К располагается выше плоскости s, а потому на П1 проекция этой части прямой видима до точки К1, другая часть прямой – невидима.

Теперь обратимся к ортогональному чертежу. Отметим на П2 точку К2 - точку пересечения s2 и а2.
Опустим из точки К2 линию связи на П1 и найдем точку пересечения с прямой а2. К1 - первая проекция точки К - точки пересечения плоскости s и прямой а.
Методом конкурирующих точек определим видимые и невидимые участки прямой а1.