Составим процедуру, определяющую, является ли список S подсписком списка L:
sublist(S, L)
Будем считать, что список L состоит из трех списков L1, S, L3, а списки S и L3 составляют список L2 (рис. 6.2).
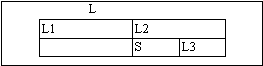
рис. 6.2
Отметим, что списки L1, S, L3 могут быть пустыми. Исходя из наглядных геометрических соображений, запишем правило принадлежности списка S списку L:
sublist(S, L):-
conc(L1, L2, L),
conc(S, L3, L2).
Это правило имеет чисто декларативный смысл. В нем утверждается, что если список L состоит из списков L1 и L2, и список L2 состоит из списков S и L3, то S есть подсписок L.
Интересно, что это правило может работать в обе стороны — если S является переменной, то правило генерирует всевозможные подсписки данного списка.
Упражнение 6.4.
Сгенерировать все подсписки списка [1,2,3], подавляя печать пустого списка [].
