При достаточно большом числе независимых опытов n частота события A сходится по вероятности к вероятности этого события, т.е.
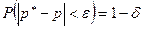, (5.2)
где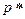 
- частота события A;
p – вероятность появления события A;
, 
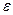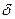- сколь угодно малые положительные числа.
Пусть производится n независимых опытов, в каждом из которых событие A может произойти с вероятностью p. В результате этих опытов можно сформировать ряд, состоящий из случайных величин - чисел появлений интересующего нас события в каждом из n опытов:
.
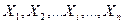Поскольку частота события A 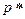представляет собой среднее арифметическое случайных величин 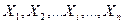и равно
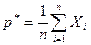, то математическое ожидание частоты события можно определить как
.
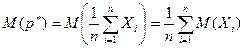Считая математические ожидания случайных величин 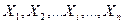одинаковыми и равными 
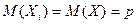, математическое ожидание частоты события будет равно
.
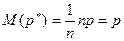Что и следовало доказать.
Пользуясь теоремой Бернулли в виде формулы (5.2) можно определить:
вероятность того, что при n испытаниях отклонение частоты события от вероятности не превзойдет величину ;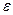
число испытаний n, необходимое для того, чтобы отклонение вероятности от частоты события не превышало 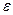при заданной вероятности P;
отклонение 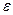частоты события от вероятности при данном числе испытаний n и заданной вероятности P.
Величину 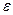называют «доверительным интервалом», а вероятность P – «надежностью» или «доверительной вероятностью».
