Пусть периодическая функция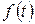 
с периодом 
разложена в ряд Фурье
. (31)
Из формулы Эйлера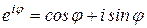 
следует, что
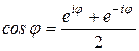и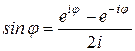 
.
Тогда 
; 
.
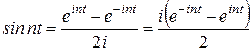Подставив эти выражения в (31) и отдельно группируя слагаемые, содержащие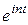 
и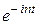 
, получим
.
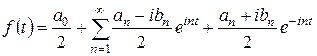Если обозначить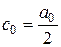 
; 
; 
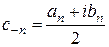, то ряд примет вид
,
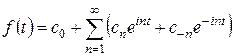а просуммировав по отрицательным значениям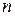 
, запишем комплексную форму ряда Фурье в окончательном виде
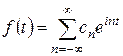. (32)
Комплексные коэффициенты Фурье 
вычисляются по формуле
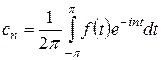
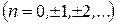. (33)
Для произвольного периода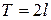 
формулы (31) и (32) принимают вид
; 
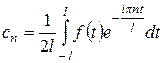
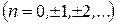. (34)
Модуль позволяет найти амплитуду 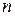-ой гармоники
; 
.
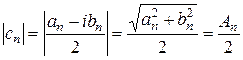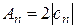Комплексная форма ряда Фурье имеет более простой вид по сравнению с формулами (24, 25). Кроме того, в ряде случаев она облегчает вычисления.
В электротехнике числа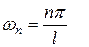 
называют волновыми числами, а их совокупность - спектром. Для ряда Фурье спектр имеет дискретный характер.
Пример 33. Разложить в ряд Фурье в комплексной форме периодическую функцию
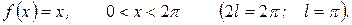
Решение. По формуле (33), интегрируя по частям, находим коэффициент Фурье для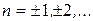 
.
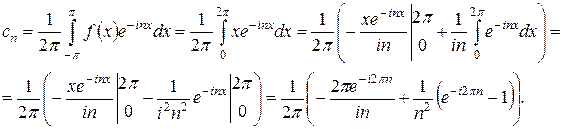
Так как
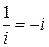и 
,
то 
.
Для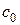 
имеем:
.
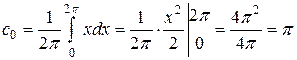Используя формулу (31), получим ряд Фурье:
.
