1)Написать уравнения касательной и нормали к кривой в заданной точке 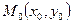 :
:
а) 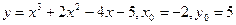 ;
;
б) 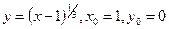 ;
;
в)  .
.
2)В какой точке касательная к параболе 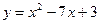
а) параллельна прямой  ?
?
б) перпендикулярна прямой 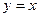 ?
?
3)Найти дифференциал  следующих функций :
следующих функций :
а) 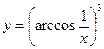 ; б)
; б) 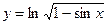 ; в)
; в) 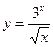 .
.
4)Вычислить приближённо:
а)  ; б)
; б) 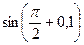 .
.
Ответы
1) а)  ; б)
; б) 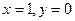 ; в)
; в) 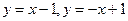 .
.
2) а) 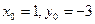 ; б)
; б) 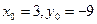 .
.
4) а) 2,25; б) 1.
Занятие №9.
Правило Лопиталя для вычисления пределов. Производная функции, заданной параметрически.
Правило Лопиталя.
1)Пусть надо найти 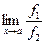 , где
, где  (или
(или 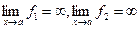 ), т.е. имеет место неопределённость вида
), т.е. имеет место неопределённость вида 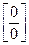 или
или 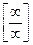 .Тогда:
.Тогда:
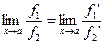 .
.
(Предполагается, что существуют производные 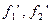 в окрестности точки
в окрестности точки 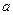 , а также существует предел, стоящий справа).
, а также существует предел, стоящий справа).
2) Пусть надо найти  , где
, где 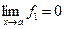 ,
, 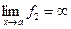 , т.е. имеется неопределённость вида
, т.е. имеется неопределённость вида 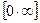 . Тогда следует сделать преобразование:
. Тогда следует сделать преобразование: 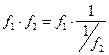 , получив неопределённость вида
, получив неопределённость вида 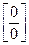 , и воспользоваться указаниями в п.1).
, и воспользоваться указаниями в п.1).
3) Пусть надо найти 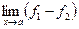 , где
, где 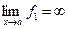 ,
, 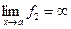 , т.е. имеется неопределённость вида
, т.е. имеется неопределённость вида 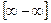 . Тогда сделать подходящее преобразование выражения
. Тогда сделать подходящее преобразование выражения 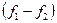 и прийти к случаю 1) или 2).
и прийти к случаю 1) или 2).
4) Пусть надо найти 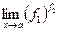 , где имеется неопределённость вида
, где имеется неопределённость вида  . Пользуясь свойствами логарифма, преобразуем данный предел:
. Пользуясь свойствами логарифма, преобразуем данный предел:
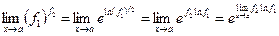
Таким образом, вычисление исходного предела сводится к вычислению предела
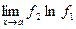 .
.
Замечание. Возможна ситуация, когда существует 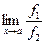 , но не существует
, но не существует 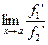 . Тогда правило Лопиталя не применимо.
. Тогда правило Лопиталя не применимо.
Производная функции, заданной параметрически.
Пусть функция 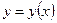 задана параметрически:
задана параметрически:
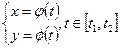
Тогда её производная 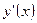 находится по следующей формуле:
находится по следующей формуле:
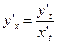 .
.
Примеры
Найти пределы, используя правило Лопиталя:
1)  ;
;
2)  ;
;
3) 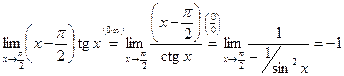 ;
;
4) 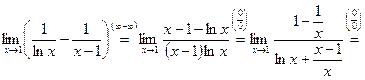
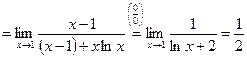 ;
;
5) 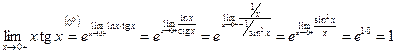 ;
;
6) 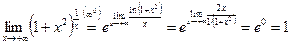 ;
;
7) 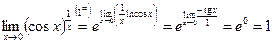 ;
;
8)Найти  для функции
для функции 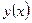 , заданной параметрически:
, заданной параметрически:
а) 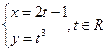 ;
;
¨  ;
;
б) 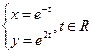 ;
;
¨ 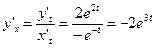 .
.