1)Если существует 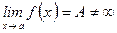 ,
, 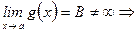
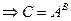 ;
;
2)Если существует  ,
,
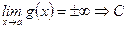 находим непосредственно
находим непосредственно
( 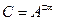 , т.е. величина
, т.е. величина 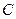 зависит от знака при символе "
зависит от знака при символе " 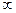 " и от того,
" и от того,  или
или 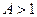 . Таким образом, либо
. Таким образом, либо 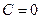 , либо
, либо 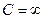 ).
).
3)Если  ,
, 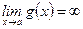 , то полагаем
, то полагаем 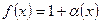 , где
, где 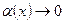 при
при 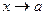 , и находим
, и находим 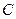 по формуле:
по формуле: 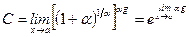 .
.
Бесконечно малые и бесконечно большие величины.
Определение 1. Если 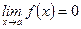
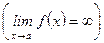 , то
, то 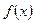 называется бесконечно малой (большой) величиной (или функцией) при
называется бесконечно малой (большой) величиной (или функцией) при 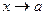 .
.
Определение 2. Если 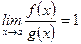 (
( 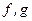 – бесконечно малые), то
– бесконечно малые), то 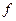 и
и 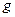 называются эквивалентными бесконечно малыми. Пишем:
называются эквивалентными бесконечно малыми. Пишем: 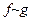 при
при 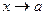 . Говорим: "
. Говорим: " 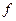 эквивалентна
эквивалентна 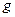 при
при 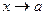 ".
".
Теорема. Пусть  ,
, 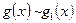 при
при 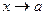 (
( 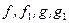 – бесконечно малые функции). Тогда:
– бесконечно малые функции). Тогда:
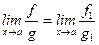 .
.
Таблица эквивалентных бесконечно малых функций при 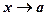 (
( 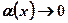 при
при 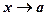 ).
).
1.  ; 8.
; 8. 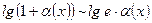 ;
;
2. 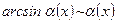 ; 9.
; 9. 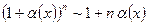
3. 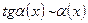 ; (
; ( 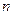 – натуральное число).
– натуральное число).
4. 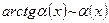 ;
;
5.  ;
;
6. 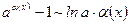 ;
;
7. 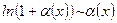 ;
;
Примеры:
1) 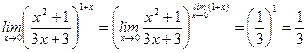 ,
,
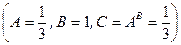 ;
;
2) 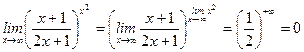 ,
,
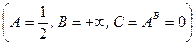 ;
;
3) 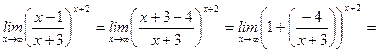
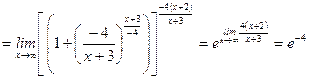 ;
;
4) 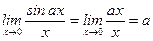 (
( 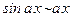 при
при 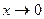 );
);
5) 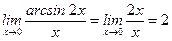 (
( 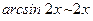 при
при 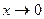 );
);
6) 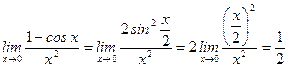 ,
,
(  при
при 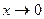 );
);
7)  (
( 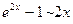 при
при 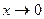 );
);
8) 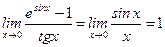 ,
,
( 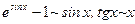 при
при 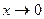 );
);
9) 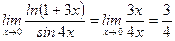 ,
,
( 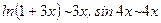 при
при 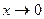 );
);
10) 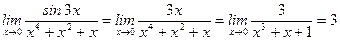 ,
,
( 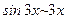 при
при 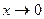 ; сделали преобразование – разделили числитель и знаменатель на "
; сделали преобразование – разделили числитель и знаменатель на " 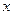 ");
");
11) 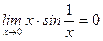 ,
,
(произведение бесконечно малой функции  на ограниченную функцию
на ограниченную функцию 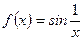 – это бесконечно малая функция, поэтому вышеуказанный предел равен нулю).
– это бесконечно малая функция, поэтому вышеуказанный предел равен нулю).
Задачи для самостоятельного решения
1) 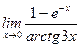 ;
2) ;
2) 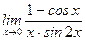 ;
3) ;
3)  ;
4) ;
4) 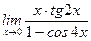 ;
5) ;
5) 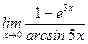 ; ;
| 6)  ;
7) ;
7) 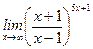 ;
8) ;
8) 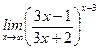 ;
9) ;
9) 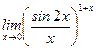 . .
|
Ответы:
1) 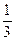 ; 2)
; 2) 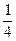 ; 3)
; 3) 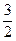 ; 4)
; 4) 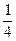 ; 5)
; 5) 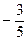 ; 6)
; 6) 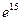 ; 7)
; 7) 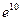 ; 8)
; 8) 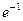 ; 9) 2.
; 9) 2.
Занятие 5.