Правило 1. Ввести новую переменную "  " так, чтобы можно было извлечь все корни, содержащиеся в функции (обычно функция содержит более одного корня; эти корни – разной степени).
" так, чтобы можно было извлечь все корни, содержащиеся в функции (обычно функция содержит более одного корня; эти корни – разной степени).
Пример.
10) 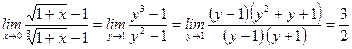 .
.
Мы сделали замену:  ; при
; при 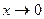
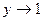 .
.
Правило 2. Перевести иррациональность из числителя в знаменатель или наоборот.
Пример.
11) 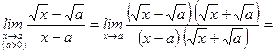
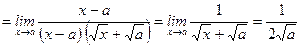 .
.
Умножили числитель и знаменатель на выражение 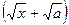 , сопряженное числителю. В результате преобразований корни из числителя "исчезли", но появились в знаменателе.
, сопряженное числителю. В результате преобразований корни из числителя "исчезли", но появились в знаменателе.
Замечание. Задачи такого типа составляются и решаются следующим образом. Берем любые числа  и
и  :
:
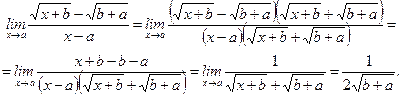
В случае примера 11: 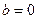 .
.
Правило 3. Разделить числитель и знаменатель на " 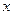 " в наивысшей степени, встречающейся в функции (возможно, после некоторых преобразований функции). Обычно в этих случаях
" в наивысшей степени, встречающейся в функции (возможно, после некоторых преобразований функции). Обычно в этих случаях 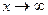 .
.
Пример.
12) 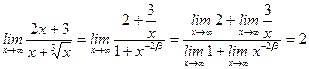 .
.
Задачи для самостоятельного решения
1)  ;
2) ;
2) 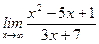 ;
3) ;
3) 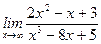 ;
4) ;
4) 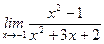 ;
5) ;
5)  ;
6) ;
6) 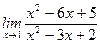 ;
7) ;
7) 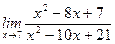 ;
8) ;
8) 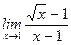 ; ;
| 9) 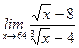 ;
10) ;
10) 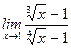 ;
11) ;
11)  ;
12) ;
12) 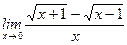 ;
13) ;
13) 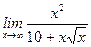 ;
14) ;
14) 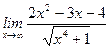 ;
15) ;
15) 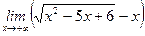 . .
|
Ответы:
1)1; 2) 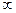 ; 3) 0; 4) -2; 5)
; 3) 0; 4) -2; 5) 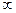 ; 6) 4; 7)
; 6) 4; 7) 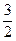 ; 8)
; 8) 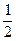 ; 9) 3;
; 9) 3;
10) 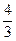 ; 11)
; 11) 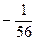 ; 12) 1; 13)
; 12) 1; 13) 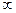 ; 14) 2; 15)
; 14) 2; 15) 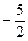 .
.
Занятие 4.