Пусть есть система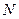 
материальных точек с массами 
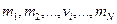имеющими координаты 
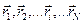. Тогда точка с координатами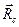 
,
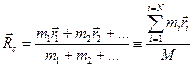где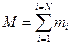 
называется полной массой системы, называется центром массы системы (иногда эту точку называют также центром инерции системы).
Рассматривая центр масс системы, вводят специальную теорему о его движении. Мы введем эту теорему в рассмотрение, сделав несколько шагов.
1. Имеются внешние силы, действующие на каждую i-ю частицу,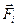 
, и внутренние силы действующие между частицами, 
.
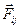2. Согласно Третьему закону Ньютона,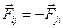 
.
3. Согласно Второму закону Ньютона для i-й частицы,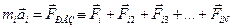 
.
4. Но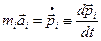 
. Получаем ряд уравнений, соответствующих правым частям:
5. 
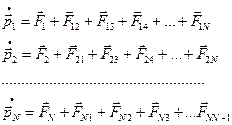
6. Сложим почленно указанные уравнения. Видно, что все внутренние силы попарно сокращаются. Остаются только внешние силы:
.
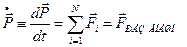Это Второй закон Ньютона для системы материальных точек.
7. Из определения центра масс следует
.
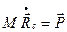8. Продифференцировав по времени, находим,
.
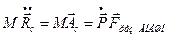Теперь теорема: Центр массы системы движется как материальная точка массы М. на которую действует результирующая сила всех внешних сил. Если эта результирующая сила равна нулю, то полный импульс системы постоянен во времени.
